什么是监督学习?
举个例子
问:已知y = ax + b,且当x = 1时,y = 2,x = 2时,y = 3。求当x = 3时y的值。
这是一个很简单的数学题,相信很多人都能很快的求出答案为 4 。
我们是怎么求出来的呢?
首先我们通过两个已知条件$ ( 1 , 2 ) , ( 2 , 3 )$ 求出了y = x + 1。然后通过y = x + 1求出了当x = 3时,y = 4。
这就是监督学习的思路,通过已知的条件和结果,求出条件与结果之间的映射关系,然后将这个映射关系运用到未知数据的回归与分类上去。
线性回归
回归问题和分类问题本质上都是探求自变量和因变量之间关系的统计学定义。不同的是,分类问题是输出离散型数据的定性输出(例如判断图片中是否有人,只会输出0或者1)。而回归问题是输出连续型变量的定量输出(例如预测房价)。
通常,当回归问题的因变量和自变量呈线性关系时,这种回归问题就被称之为线性回归。我们在“什么是监督学习”中举的例子就是一种线性回归方程。因回归方程的自变量(特征)只有一个,所以我们称之为一元线性回归或简单回归。自变量有多个的线性回归,则称为多元线性回归或多元回归。
函数模型
$$
h_w(x^i) = w_0 + w_1x_1 + w_2x_2 + … +w_nx_n(w_0称为偏置项)
$$
$$
h_w(x_i) = W^TX
$$
$$
X = \begin{bmatrix}
1 \\
x_1 \\
x_2 \\
… \\
x_n \\
\end{bmatrix}
W = \begin{bmatrix}
w_0 \\
w_1 \\
w_2 \\
… \\
w_n \\
\end{bmatrix}
$$
回到我们在“什么是监督学习”中举的例子,我们有训练集$( 1 , 2 ) , ( 2 , 3 )$,则进行第一次训练时
$$
X = \begin{bmatrix}
1 \\
1 \\
\end{bmatrix} W = \begin{bmatrix}
b \\
a \\
\end{bmatrix}
$$
第二次训练时
$$
X = \begin{bmatrix}
1 \\
2\\
\end{bmatrix} W = \begin{bmatrix}
b \\
a \\
\end{bmatrix}
$$
损失函数
损失函数(lost function)或者称为代价函数(cost function)在机器学习中主要作为对学习进行优化的参考值。简单说就相当于是预测结果与实际结果的差距。我们对机器学习的优化就旨在缩小这个损失函数的值。
我们通常用到的损失函数主要有最小二乘法
$$
J(W) = \frac{1}{2M}\sum_{i = 0}^{M} (h_w(x^i) - y ^i)^2 = \frac{1}{2M}(XW - y)^T(XW - Y)
$$
梯度下降
综述
上文说到,我们要对机器学习进行优化,减小损失函数的值,而梯度下降就是一种比较常见的优化算法。
首先,我们取一个初始点,我们希望能够下到山谷的最低点,最快的方式便是向着坡度最陡的地方走。于是我们一步一步往下走,每走一步就重新找到在这个位置向下最陡的方向,于是,我们就像下图一样走到了一个谷底。
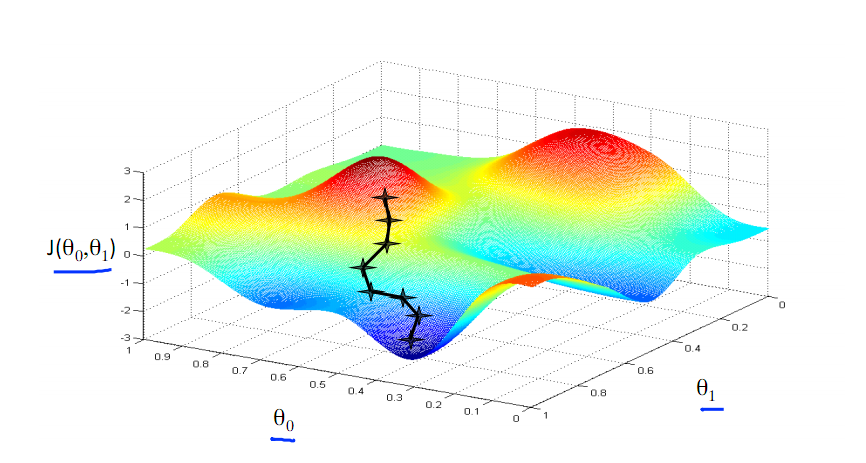
但相对的,如果我们一开始的起始点选择的是另一个地方,则有可能会走到另一个谷底。
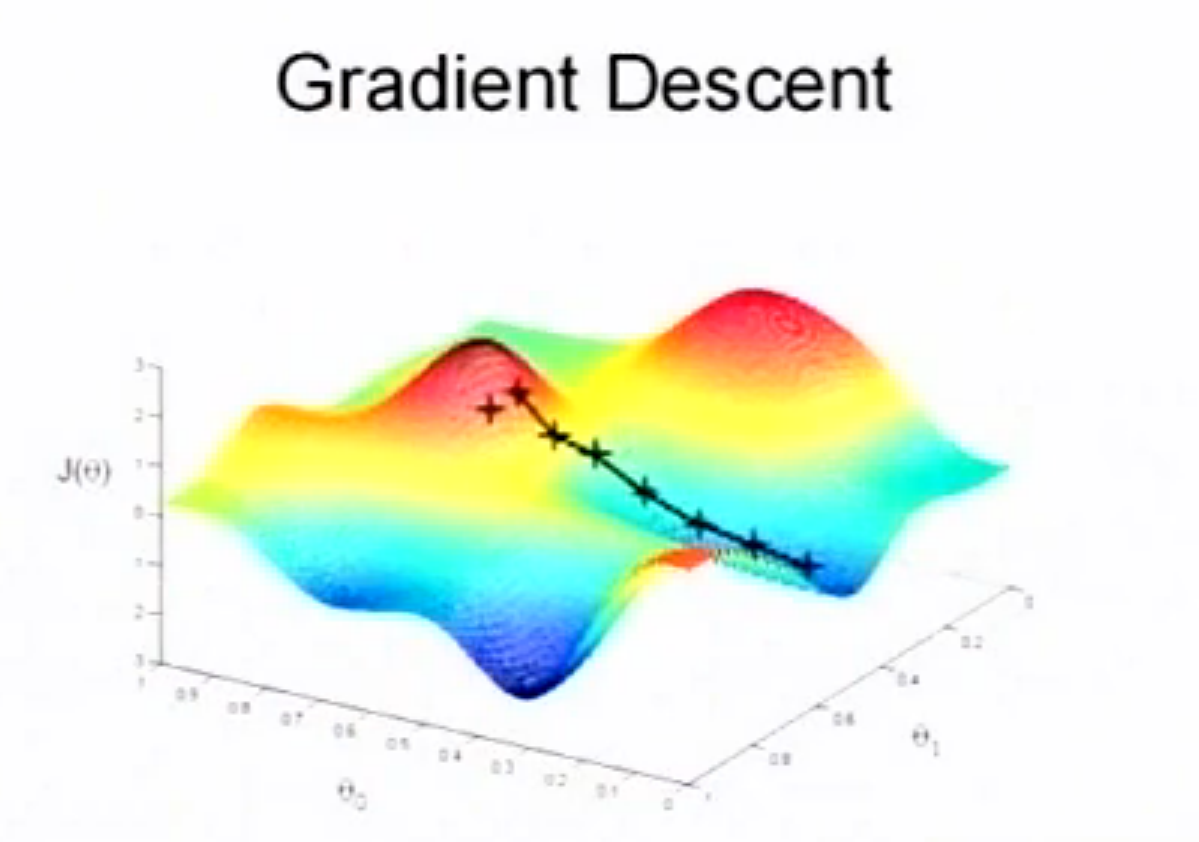
从这里我们可以看出,起始点的选择在很大程度上会决定梯度下降算法达到谷底的位置。而我们无法保证能够达到全局的最低点,但可以保证达到局部最低点。
$$
\theta_j := \theta_j - \alpha\frac{\partial}{\partial\theta_j}J(\theta_0,\theta_1)
$$
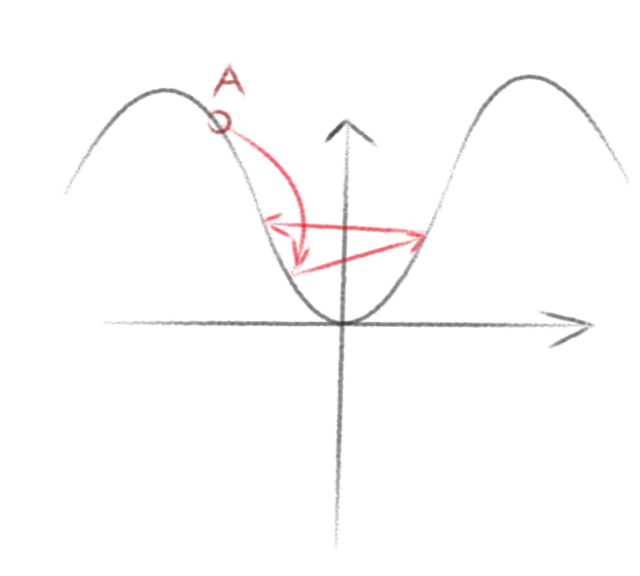
二维化简述
我们将梯度下降当做一个二维图来重新描述其原理。
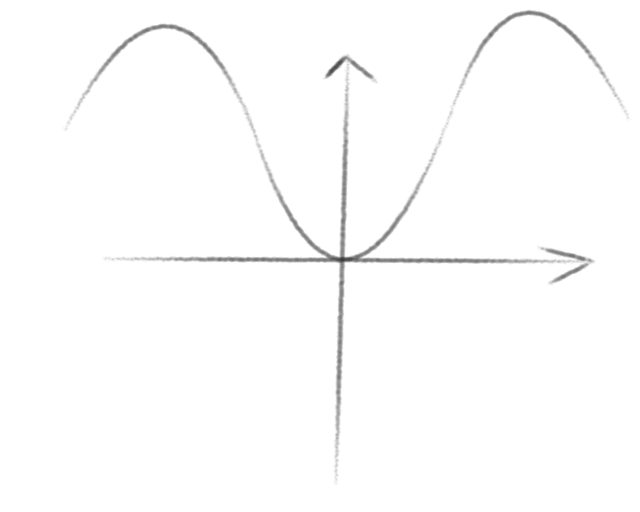
假设,我们随机在A点,此时,我们求出其下降最陡的方向,并向这个方向移动
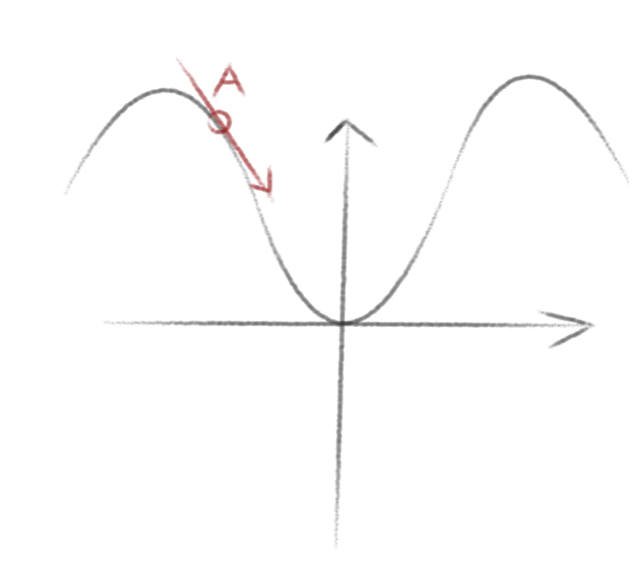
于是我们又到达了B点,继续向下移动便会到达谷底。
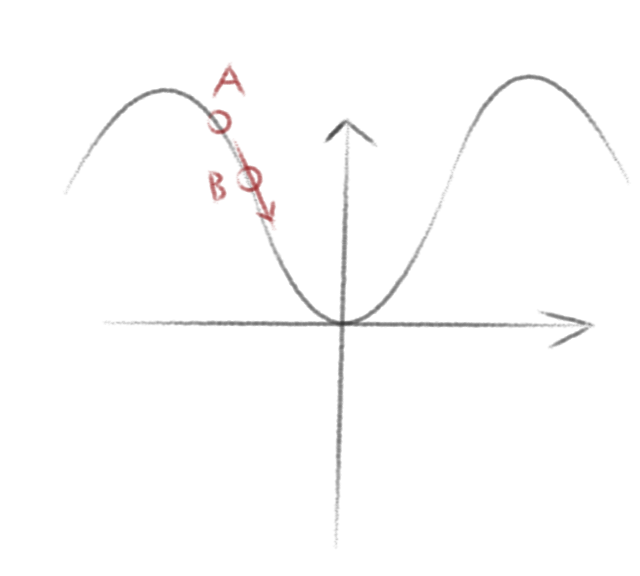
但是这里要注意两个问题,一个是谷底并不是只有一个,所以我们到达的并不一定是全局最低点,通常只是局部最低点。
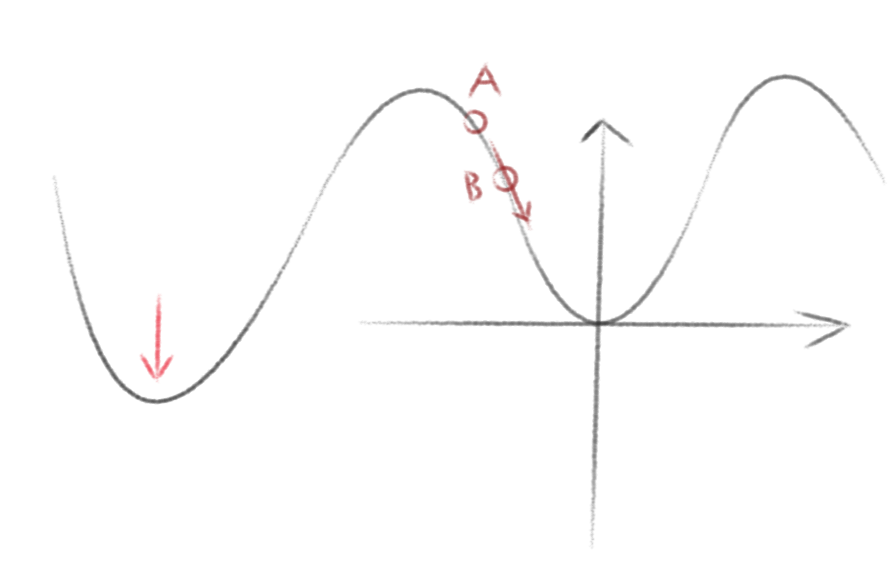
另一个则是如果我们移动时步长选择的太大,则有可能会错过局部最低点