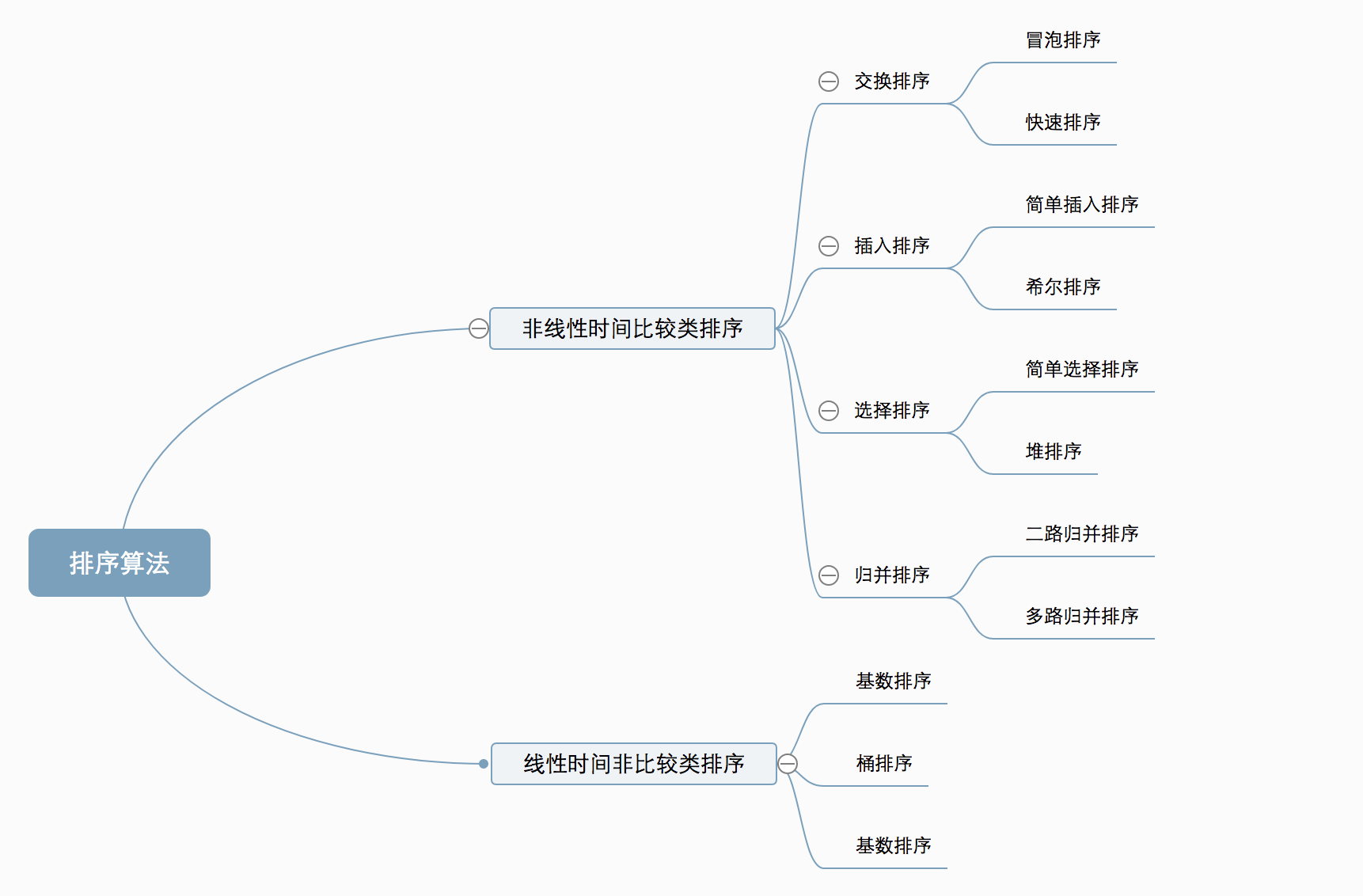
简单选择排序
在java编程中我们经常遇到排序问题,在我们刚刚学习编程时,我们通常使用的是以下的方式进行排序:
int temp;
for(int i = 0; i < data.length() - 1;i++){
for(int j = i + 1;j < data.length();j++){
if(data[j] > data[i]){
temp = data[j];
data[j] = data[i];
data[i] = temp;
}
}
}
这种排序方式就是我们最基础的选择排序。
选择排序的思想是所有排序算法中最简单易懂的:循环找出数组中最小的数置于最前。但选择排序存在两点缺陷:
- 有许多不必要的数据交换操作
例如:将数组{3,1,5,4,0}进行升序排序,使用选择排序需要经历以下步骤
- {1,3,5,4,0} 将3与1进行交换
- {1,3,5,4,0} 5大于1,不进行交换
- {1,3,5,4,0} 4大于1,不进行交换
- {0,3,5,4,1} 0小于1,进行交换操作
到这里就会发现,在执行到第四步时,只因为0大于1,就将0置于最后,而我们需要的操作仅仅是将0置于最前。这样即增加了之后的操作数,也增加了交换次数。
- 不稳定排序算法
当数组中的相同值在排序后的相对位置不变时,我们说这种排序算法是稳定排序算法。
在选择排序中,举例:{3,3,1}
我们在进行排序时,会将第一个3与1进行交换,两个3的相对位置发生了改变,故说它是不稳定排序算法。
算法复杂度:$O(n^2)$
循环次数:$\frac{n(n-1)}{2}$
冒泡排序
冒泡排序的思想也比较简单,也是像选择排序一样存在两个循环。在第一次循环时,从倒数第二个元素比较到第一个元素,若当前元素的值,与当前元素+1位置的值不构成排序关系时,就将两元素进行交换。第二次循环从倒数第二个元素比较到第二个元素……依次类推。
假设数组{21,34,12,34,78,12,34},要使用冒泡排序进行由小到大排序,则会经历以下步骤:
- {21,34,12,34,78,12,34}
- {21,34,12,34,12,78,34}
- {21,34,12,12,34,78,34}
- {21,34,12,12,34,78,34}
- {21,12,34,12,34,78,34}
- {12,21,34,12,34,78,34}
……
可以看出,整个排序过程中,最小的元素像冒泡一样从最后浮到的最前,所以这种排序算法被称为冒泡排序。
将这种算法落实到代码上就是:
for(int i = 0;i < data.length - 1;i++){
for(int j = data.length - 2;j >= i;j--){
if(data[j] > data[j + 1]){
int temp = data[j];
data[j] = data[j+1];
data[j+1] = temp;
}
}
}
当然,这时从后向前的冒泡排序,根据同样的理论,我们也可以写出从前往后的冒泡操作:
for(int i = 0;i < data.length - 1;i++){
for(int j = 0;j < data.length - 1 - i;j++){
if(data[j] > data[j + 1]){
int temp = data[j];
data[j] = data[j+1];
data[j+1] = temp;
}
}
}
与选择排序不同,冒泡排序的操作中必然会导致两相同元素靠在一起,这时我们不对相同元素进行位置交换,则排序结束后相同元素的相对位置不变,故冒泡排序是一种稳定排序算法。
算法复杂度
当n个元素的数组排序开始时就是顺序排列,则需要进行n - 1次比较、0次移动即可完成整个排序,此时的比较次数C和移动次数M最小:
$$C_{min} = n - 1$$
$$M_{min} = 0$$
故冒泡排序最好算法复杂度为$$O(n)$$
当数组排序开始时是逆序排列,则需要进行n-1次循环,第i次循环需要进行n-1-i次比较,每次比较需要进行三次移动,此时当比较次数和移动次数最大:
$$C_{max} = \frac{n(n-1)}{2} = O(n^2)$$
$$M_{max} = \frac{3n(n-1)}{2} = O(n^2)$$
故冒泡排序最坏算法复杂度为$$O(n^2)$$
因此,冒泡排序算法当平均算法复杂度为$$O(n^2)$$
快速排序
快速排序与冒泡排序都属于交换排序。快速排序是对冒泡排序对一种优化。快速排序对主要思想是挖坑填数和分治法。
分治法就是将需要解决的问题转化为更小的子问题,并将子问题逐个击破,将子问题的解进行合并,合并为原问题的解。
快速排序的基本原理是:在需要排序的数组中选取一个数作为基准数,通过两个游标分别从左向右、从右向左进行扫描,将达成排序关系A的放在基准数左边,达成排序关系B的放在基准数右边。然后左右分串再次进行类似操作。
下面举一个例子进行详细说明:
欲使用快速排序对数组{12,3,22,51,13,7,10,11}进行升序排序:
1.
| 基准数 | i | j | |||||
|---|---|---|---|---|---|---|---|
| 12 | 3 | 22 | 51 | 13 | 7 | 10 | 11 |
首先要选择基准数,为了方便起见,我们使用数组第一个值为基准数,这时设置两个游标i和j,分别从左向右、从右向左进行扫描。
2.
| 基准数 | i | j | |||||
|---|---|---|---|---|---|---|---|
| 12 | 3 | 22 | 51 | 13 | 7 | 10 | 11 |
此时,i移动到22时,22大于基准数12,故停止扫描,j开始移动。j移动到11时,发现11小于基准数12,故停止扫描。
3.
| 基准数 | i | j | |||||
|---|---|---|---|---|---|---|---|
| 12 | 3 | 11 | 51 | 13 | 7 | 10 | 22 |
将两个数进行交换,交换后,继续从i开始扫描,并重复之前的操作。
4.
| 基准数 | i | j | |||||
|---|---|---|---|---|---|---|---|
| 12 | 3 | 11 | 10 | 13 | 7 | 51 | 22 |
10和51进行了交换。
5.
| 基准数 | i | j | |||||
|---|---|---|---|---|---|---|---|
| 12 | 3 | 11 | 10 | 7 | 13 | 51 | 22 |
7和13进行了交换。
6.
| i | j | ||||||
|---|---|---|---|---|---|---|---|
| 7 | 3 | 11 | 10 | 12 | 13 | 51 | 22 |
当i和j相遇时,将基准数与i交换,此时基准数左边都是小于12的数,右边都是大于12的数。再将左右的数分成两个字串,使用递归再次进行之前的操作,知道字串不能再分,则完成了排序。
基准数的选择
在我们通常情况下,基准数的选择主要有以下几种方式:
- 使用第一个或最后一个数作为基准数,这种选择方式比较方便,但当遇到原本就是正序或倒序排列的数组时,就会降低算法性能。
- 随机选取数字作为基准数,这种选取方式较为安全。
- 三数取中,将第一个数、最后一个数、中间的数排列后取中值,也在一定程度上减少了复杂化的危险性。
以下使用三数取中法为例:
public class Main{
public static void main(String[] args) {
int[] data = new int[]{12,3,22,51,13,7,10,11};
quicksort(data,0,data.length - 1);
System.out.println(Arrays.toString(data));
}
public static void quicksort(int[] data,int left,int right){
if(left >= right)
return;
int medium = (left + right) / 2; //求出中值的位置
if(data[left] > data[right]) //保证左端的值较小
swap(data,left,right);
if(data[medium] > data[right]) //保证中间的值较小
swap(data,medium,right);
if(data[medium] > data[left]) //保证左端的值为中值
swap(data,medium,left);
int pivotvalue = data[left];
int i = left;
int j = right;
while(i < j){
while(data[i] <= pivotvalue="" &&="" i="" <="" j)="" i++;="" while(data[j]="">= pivotvalue && i < j)
j--;
if(i < j)
swap(data,i,j);
}
int temp = 0;
if(data[i] > data[left]) //判断游标值大小
temp = i - 1;
else
temp = i;
swap(data,temp,left);
quicksort(data,left,temp - 1);
quicksort(data,temp + 1,right);
}
public static void swap(int[] data,int a,int b){
int temp = data[a];
data[a] = data[b];
data[b] = temp;
}
}
平均算法复杂度:$O(nlogn)$
堆排序
堆排序主要针对的是“堆”这种数据结构。它是一种选择排序。
堆
堆(heap)是计算机科学中的一类数据结构,它的表现形式是一棵完全二叉树的层序遍历数组。
堆结构与完全二叉树的不同在于:
- 堆中的节点总是不大于或不小于其父节点的值,即堆结构存在有序性。
所以我们可以说:
- 堆一定是完全二叉树。
- 完全二叉树不一定是堆。
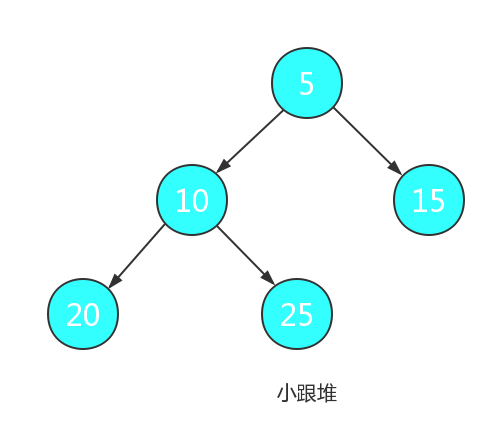
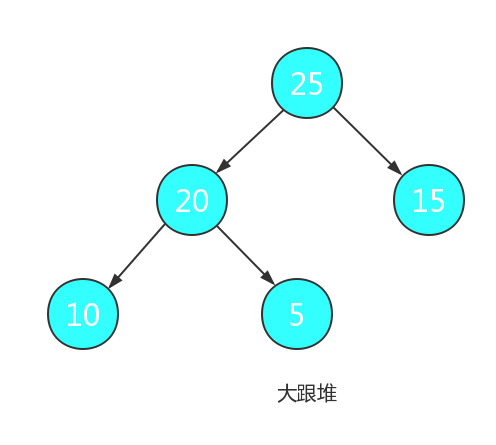
堆通常分为两种:根节点为最小值的堆为小根堆(最小堆),根节点为最大值的堆为大根堆(最大堆)。
堆排序的主要原理为:
- 从下向上遍历每个非叶节点,使它与子节点形成堆关系。
- 将根节点与最后一个节点进行互换,此时数组最后一位为最大/最小值。
- 将除去原根节点之外的数据重复以上操作,逐步将每次的最大/最小值沉入数组后方,完成排序。
下面使用图示进行详细讲解:
例如,需要排序的数组为{12,3,5,14,8},我们使用堆排序进行升序排序,我们首先将数组构建为如下二叉树:
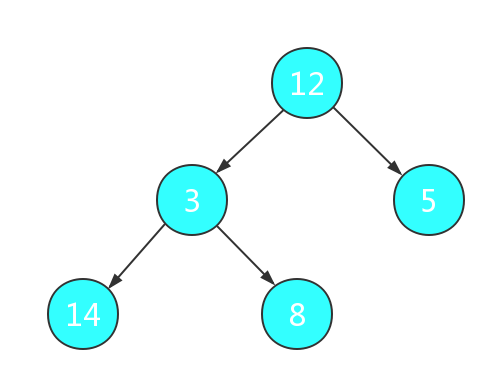
因为是升序排序,所以我们考虑构建大根堆,首先找到最后的非叶节点,将它与两子节点节点进行比较,最大值交换到当前位置:
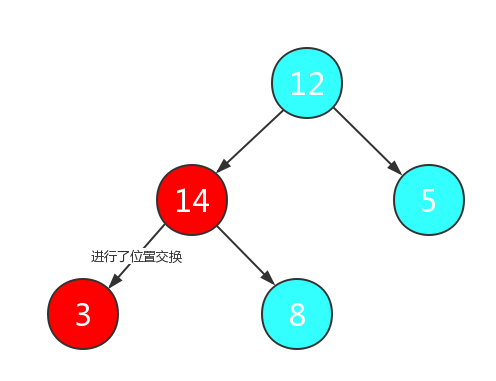
然后继续向上寻找非叶节点,此时非叶节点为跟节点,重复之前的操作:
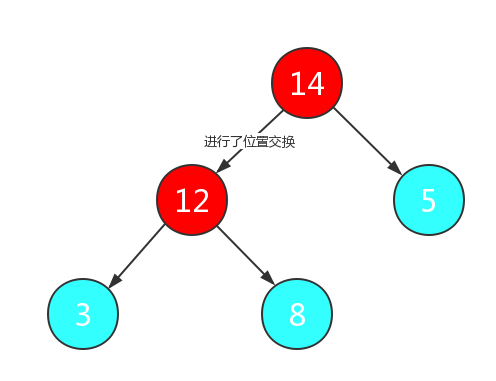
我们将此时的根节点,也就是数组中的最大值与最后一个节点进行交换:
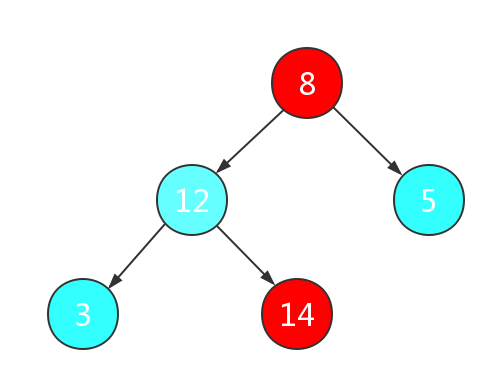
此时的数组也就变成了{8,12,5,3,14},数组的最大值沉到了最后一位。接下来,不考虑最后一位,继续重复之前操作,即可完成排序。
使用代码实现如下:
public class Main{
public static void main(String[] args) {
int[] data = new int[]{12,3,22,51,13,7,10};
sort(data);
System.out.println(Arrays.toString(data));
}
public static void sort(int []arr){
//1.构建大顶堆
for(int i=arr.length/2-1;i>=0;i--){
//从第一个非叶子结点从下至上,从右至左调整结构
adjustHeap(arr,i,arr.length);
}
//2.调整堆结构+交换堆顶元素与末尾元素
for(int j=arr.length-1;j>0;j--){
swap(arr,0,j);//将堆顶元素与末尾元素进行交换
adjustHeap(arr,0,j);//重新对堆进行调整
}
}
/**
* 调整大顶堆(仅是调整过程,建立在大顶堆已构建的基础上)
* @param arr
* @param i
* @param length
*/
public static void adjustHeap(int []arr,int i,int length){
int temp = arr[i];//先取出当前元素i
for(int k=i*2+1;ktemp){//如果子节点大于父节点,将子节点值赋给父节点(不用进行交换)
arr[i] = arr[k];
i = k;
}else{
break;
}
}
arr[i] = temp;//将temp值放到最终的位置
}
/**
* 交换元素
* @param arr
* @param a
* @param b
*/
public static void swap(int []arr,int a ,int b){
int temp=arr[a];
arr[a] = arr[b];
arr[b] = temp;
}
}
可以看出,虽然此算法叫堆排序,但实际上经过调整,对不构成完全二叉树的数据依旧可以进行排序。
堆排序算法的最优、最差、平均算法复杂度均为:$O(nlogn)$
堆排序与基本选择排序一样,均为不稳定排序算法。
参考文章:
图解排序算法(三)之堆排序
简单插入排序
简单插入排序又称直接插入排序,也是一种较为简单的排序方式。
它的主要思路是,将数组中元素,依次放入有序表中,每次插入新元素,就将它与已有元素进行比较,将排序逻辑靠后的元素位置加一,将新元素插入。
代码如下:
public class Main{
public static void main(String[] args) {
int[] data = new int[]{12,3,22,51,13,7,10};
data = simpleInsertSort(data);
System.out.println(Arrays.toString(data));
}
private static int[] simpleInsertSort(int[] data) {
if(data.length <= 1)="" return="" data;="" int[]="" result="new" int[data.length];="" result[0]="data[0];" for(int="" i="1;i" <="" data.length;i++){="" int="" pos="0;" j="i" -="" 1;="">= 0 ;j--){
if(result[j] <= data[i])="" {="" pos="j" +="" 1;="" break;="" }="" else="" result[j="" 1]="result[j];" result[pos]="data[i];" return="" result;="" <="" code="">当原数组为正序时,每次插入都只需要比较一次,所以最优算法复杂度为:$O(n)$
当原数组为倒序时,每次插入都需要与之前当所有数据进行比较,所以最差算法复杂度为:$1+2+3+…+(n-1) = \frac{1+(n-1)}{2} \times n =O(n^2)$
平均算法复杂度为:$O(n^2)$
希尔排序
希尔排序是对简单插入排序的一种优化排序算法,也被称为减小增量排序,它是最早突破$$O(n^2)$$复杂度的一批算法。
希尔排序的主要思路是:首先选定一个增量,按照增量来将原有数组划分为多个子数组,分别将各个子数组进行插入排序,然后不断减少增量,重复之前的步骤,直到增量减小为1时完成排序。
图解如下:
| 增量为4 | |||||||
|---|---|---|---|---|---|---|---|
| 4 | 3 | 1 | 6 | 5 | 2 | 8 | 7 |
| 第一次排序 | |||||||
|---|---|---|---|---|---|---|---|
| 4 | 2 | 1 | 6 | 5 | 3 | 8 | 7 |
| 增量为2 | |||||||
|---|---|---|---|---|---|---|---|
| 4 | 2 | 1 | 6 | 5 | 3 | 8 | 7 |
| 第二次排序 | |||||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 4 | 3 | 5 | 6 | 8 | 7 |
| 增量为1 | |||||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 4 | 3 | 5 | 6 | 8 | 7 |
| 第三次排序 | |||||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
增量的选择
增量的选择与减小规则应该按照实际情况进行规划,我们这里使用最简单的方式:初始增量为数组长度的一般,每次增量减小为原先增量的一半。在进行分段排序时,我们可以使用有序数组插入的方式,也可以使用交换方式。
public class ShellSort {
public static void main(String []args){
int []arr ={1,4,2,7,9,8,3,6};
sort(arr);
System.out.println(Arrays.toString(arr));
int []arr1 ={1,4,2,7,9,8,3,6};
sort1(arr1);
System.out.println(Arrays.toString(arr1));
}
/**
* 希尔排序 针对有序序列在插入时采用交换法
* @param arr
*/
public static void sort(int []arr){
//增量gap,并逐步缩小增量
for(int gap=arr.length/2;gap>0;gap/=2){
//从第gap个元素,逐个对其所在组进行直接插入排序操作
for(int i=gap;i=0 && arr[j]0;gap/=2){
//从第gap个元素,逐个对其所在组进行直接插入排序操作
for(int i=gap;i=0 && temp 其最坏时间复杂度依然为$O(n^2)$,一些经过优化的增量序列如Hibbard经过复杂证明可使得最坏时间复杂度为$O(n^{\frac{3}{2}})$
本段参考:
更新记录
| 更新时间 | 更新内容 |
|---|---|
| 2018年5月14日 | 选择排序 |
| 2018年5月15日 | 冒泡排序 |
| 2018年5月16日 | 快速排序 |
| 2018年5月17日 | 堆排序 |
| 2018年5月17日 | 简单插入排序 |
| 2018年5月23日 | 希尔排序 |



